Уверен, вы любите школьную математику и с удовольствием решаете сложные задачки, но в этой статье речь пойдет не совсем о математике, мы разберем и рассмотрим что такое математические выражения в Python.
Математические операции с целыми и вещественными числами
Прежде чем приступим разбираться, мы должны запомнить, что математические действия применяют только к числовым типам данных. Какие бывают типы данных в Python мы писали ранее, здесь просто вспомним:
- Целочисленные — int;
- Вещественные, или еще их называют с плавающей точкой — float;
- Комплексные числа — complex.
Операция сложения
a = 5 b = 7 c = a + b print(c) # 12
Операция вычитания
a = 5 b = 7 c = a - b print(c) # -2
Операция умножения
a = 5 b = 7 c = a * b print(c) # 35
Операция деления
a = 5 b = 7 c = a / b print(c) # 0,7142857142857143
Как видим, в результате деления 2-х целых чисел мы всегда получаем вещественное число, с типом данных float
Операция возведения в степень
a = 5 b = 3 c = a ** b print(c) # 125
Обратите внимание, операция возведения в степень в Python — ** (две звездочки)
Операция целочисленного деления
a = 5 b = 2 c = a // b print(c) # 2
Обратите внимание, операция целочисленного деления в Python это // (два слеша) и результатом ее всегда будет тип данных int, то есто вся дробная часть просто отбрасывается!
На этом, математические выражения в Python не заканчиваются! Есть еще одна очень интересная операция:
Операция нахождения остатка от деления
Обозначается она как знак процента, т.е. %, но ничего общего с нахождением процентов она не имеет!
На самом деле, результат операции нахождения остатка от деления — это ни что иное, как то число, что осталось после деления без остатка. Т.е., если мы делим 5 / 2, целых будет 2, а в остатке будет 1.
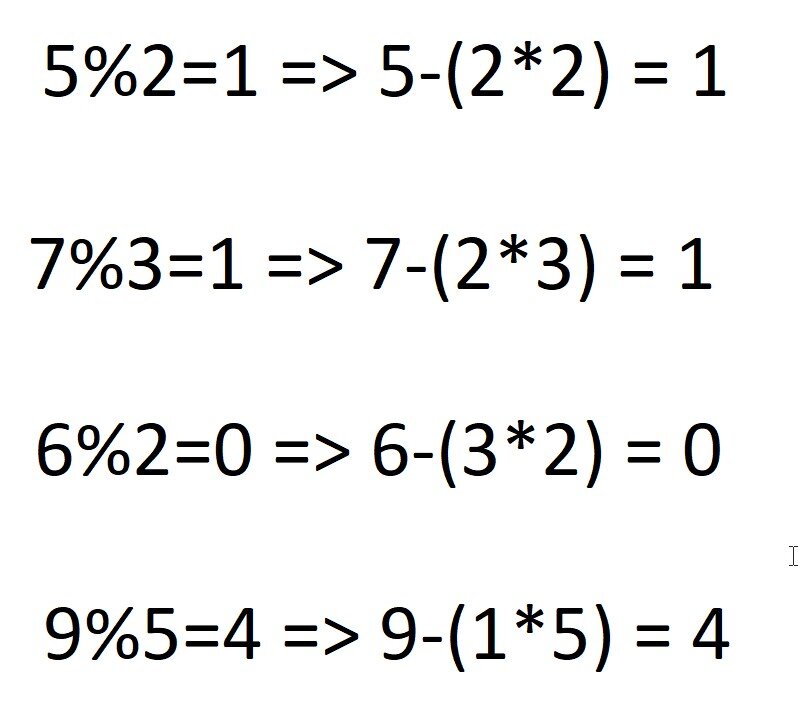
Математические операции с комплексными числами
Что бы создать комплексное число можем либо сразу его записать как таковое, либо воспользуемся функцией complex(a, b), где a — действительная часть, b — мнимая часть.
z = 1 + 2j print(z) # (1+2j) x = complex(3, 2) print(x) # (3+2j)
С комплексными числами можно производить математические действия, складывать, вычитать, умножать, делить и возводить в степень.
z = 1 + 2j x = complex(3, 2) x + z # (4+4j) x - z # (2+0j) x * z # (-1+8j) x / z # (1.4-0.8j) x ** z #(-1.1122722036363393-0.012635185355335208j) x ** 3 # (-9+46j)
Что бы извлечить действительную часть комплексного числа применяем real, а если нам нужна мнимая часть — метод imag
x = complex(3, 2) print(x) # (3+2j) print(x.real) # 3.0 print(x.imag) # 2.0





